一种优化Freespace检测效能的智驾感知提升算法
出品 | 焉知汽车
高级驾驶辅助系统（ADAS）开发中最关键的问题之一是汽车周围环境的描述方式。环境可以分为动态和静态部分。第一个用于描述所有可移动物体，如汽车或汽车等。行人。第二个代表静态障碍物，如护栏、路缘石、建筑物或障碍物等。为了在拥挤的环境中自由移动，需要提供有关所有周围障碍物的高精度信息。有一个可用于此目的的广泛表示，即 2D和 3D 网格、区间图、原始结构和轮廓。
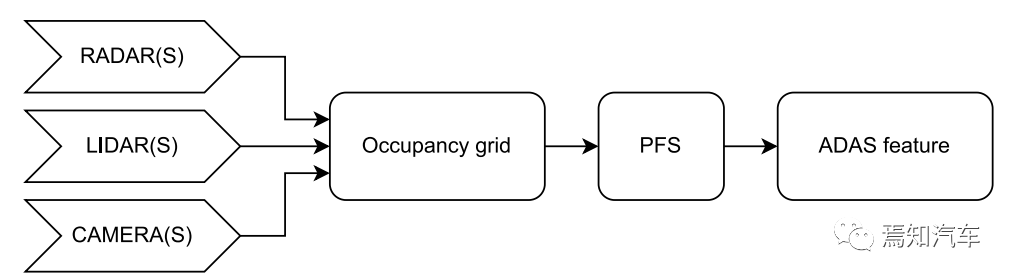
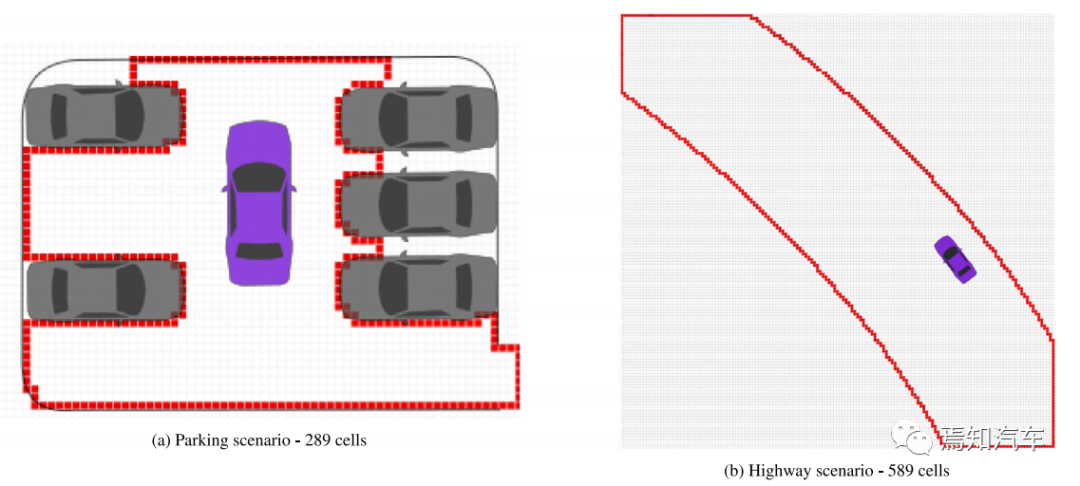
一旦完成图像处理并确定边界像素，单元定义的边界将通过参数曲线（b 样条曲线）来近似。它由状态空间模型表示为：
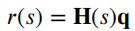
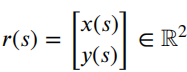
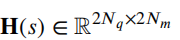表示观测矩阵，其中的q表示为：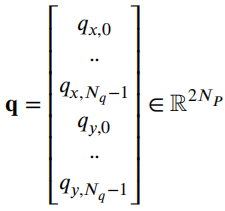
是作为一组2维B样条控制点的状态向量，Nq是控制点的数量，Nm是测量点的数量，qx,n表示第n个控制点的纵向位置，qy,n表示第n 个控制点的横向位置。
使用信息滤波器在每个周期递归地完成近似，这对于大量测量点而言比经典卡尔曼滤波器计算效率更高。即使进行了这种优化，大量测量仍然是一个问题（模型被视为单个 2D 测量，并用于更新两个样条函数x(s)和 y(s)。此外，为了能够使用信息过滤器，必须预先在每个循环进行计算观测矩阵H(s)，其大小（行数）严格取决于测量次数。
针对一般点云的数据缩减，人们提出了许多方法。比如，通过基于所需点数缩减的比率搜索点子集来实现。
本文介绍的方法最小化了原始集和缩减子集之间的几何偏差。还有另一种方法由两个步骤组成。第一步，通过八叉树结构对点云进行正则化和压缩。第二步，点云根据曲率规则进行简化。这种方法与八叉树结构有一些相似之处。还有一些基于kmeans聚类算法的自适应简化方法。唯一的数据缩减（向下选择）在曲线拟合上下文中找到的算法是“正切函数”专用于非均匀有理B样条 (NURBS) 近似的方法”。
在该方法中，向下选择步骤包括三个连续原始测量点的局部二次插值，以查找沿定义的二次插值的斜率符号的变化空间轴。如果检测到斜率变化，则向下选择最近的测量点，然后将其做为 NURBS 的控制点。否则，不向下选择任何测量点。
解决方案
为了解决上一节中描述的大量测量的问题，这里提出了三种测量下选算法。
1、测量点分布均匀
PFS算法的一个假设是所有测量点均匀分布。这意味着样条曲线和测量点的起点和终点相对应。基于此，最简单（朴素）的下选算法是取每个第k测量点（mx,k，my,k），并根据以下公式：
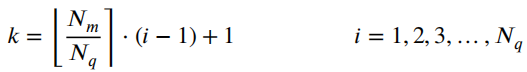
该解决方案的缺点是它强制样条线的每个控制点只有一个测量点，这可能不足以准确反映周围环境。
2、“Line”向下选择
本段和下一段中描述的算法集中于以下思想：仅保留行测量的特征点，并过滤掉所有冗余的点，即那些不提供有关边界形状的有价值信息的点。
“线”向下选择是通过使用线性方程y=ax+b来过滤特征点（即单元格表示形式），其想法是拒绝尽可能多的共线点。整个边界被分为相同长度的部分，部分端点是用虚拟线连接。
然后，对于该部分（其端点之间）内的每个点（像素），计算到该线的距离（例如下图中绿色特征点连接的红线部分）。如果该点的距离较大于阈值，该点被视为特征点。
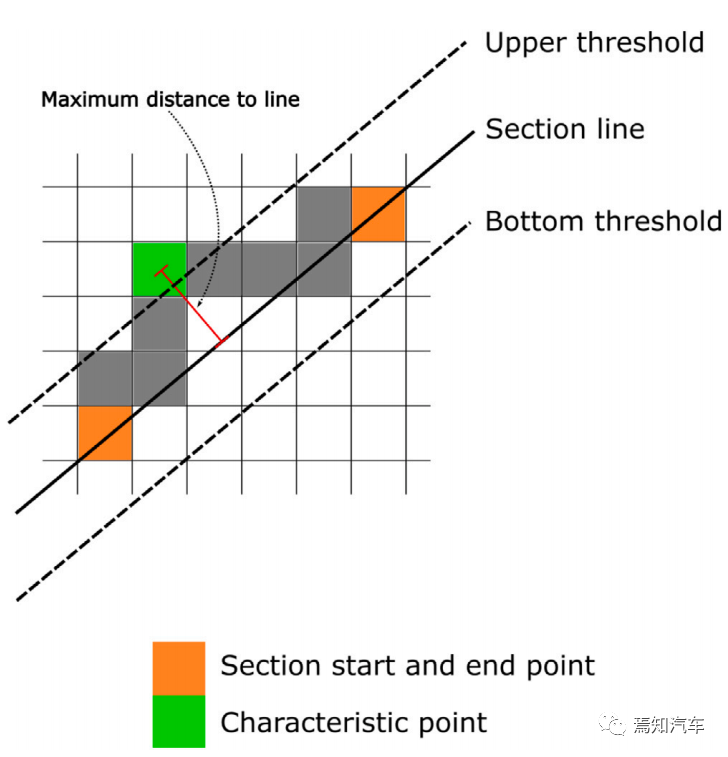
所有比该阈值更接近直线的像素都被认为是冗余的。一段的每个终点也是下一段的起点，也被视为特征点，保留这些点的好处是每个样条控制点（假设截面长度足够小）至少有一个支撑测量点。该算法通过寻找部分端点之间的特定点来扩展简单统一方法。
3、边界方向的下采样
为了限制额外操作的数量，寻找特征点，基于“方向”的方法仅限于对像素进行简单操作。其想法是检查从前一个像素到感兴趣像素的移动方向是否正确。并且从感兴趣的像素到下一个像素，按照该顺序，是相同的。如果不同，则中间点被视为特征点。例如，如果所考虑的点之前和之后的移动方向是往右上角（见下图所示）的，则该点不被标记为特征点。但如果连续移动方向不同，则该点被标记为特征点。
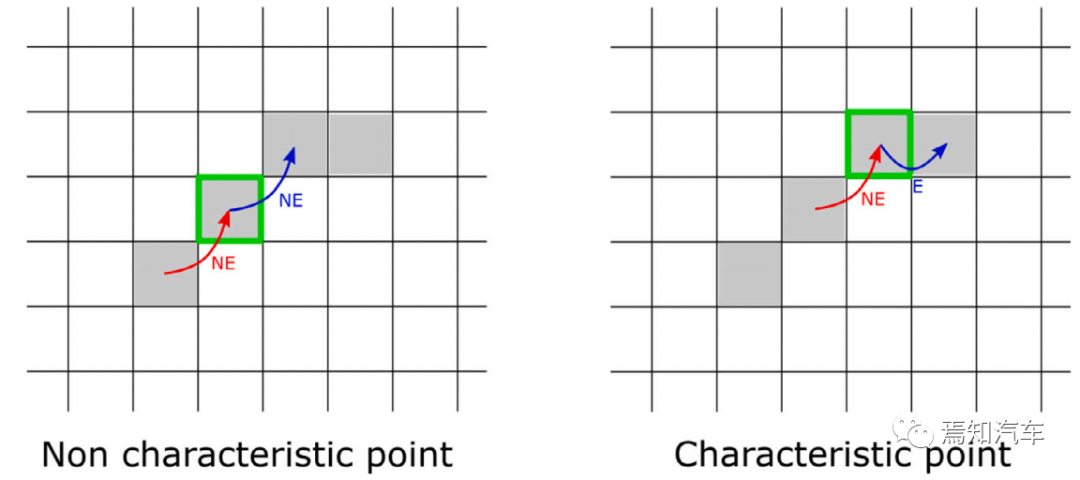
算法优势的不同维度对比
为了避免操作系统对计算时间估算的影响，需要重复测试多次并取平均值。最终的计算时间在下一节中给出，是所有场景中最长的时间。比较最长时间而不是平均值更有价值，因为无论汽车周围环境多么复杂，每种算法都应该在有限的时间内完成其工作。
1、降采样大小
如下图表示包含每种方法每个周期的平均测量点数量。正如预期的那样，与不使用降选方法相比，Original表示所提出的下采样方法中每个周期的平均测量点数量。本文提出的方法显着减少了测量点的数量，“Uniform”算法平均值减少了 16.74 倍，基于“Line”的算法平均值减少了 11.61，基于“Direction”方法则只有 2.15。
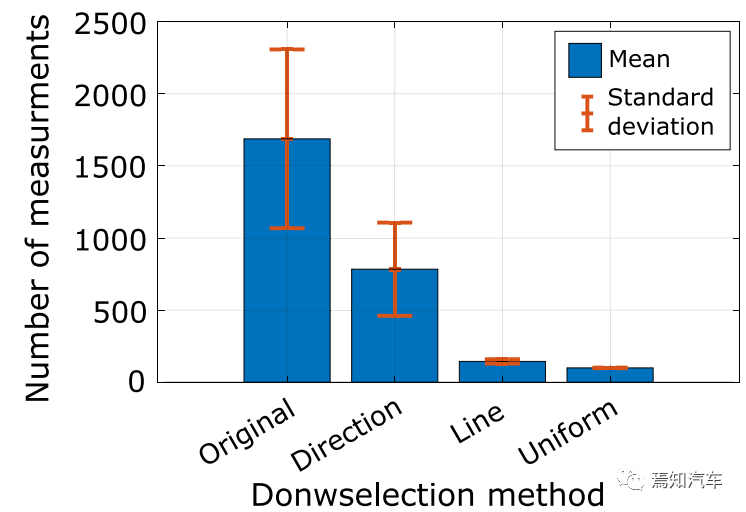
因此，大多数点都是使用“Uniform”方法过滤的。过滤的点数正好是使用的样条控制点的数量（即100）。“Line”方法作为前一种方法的扩展，添加了重要的点。这两种方法比前一种方法要好得多。“Direction”方法仅将测量点的数量减少大约 2 倍。其主要原因是该方法实际上表现得更像插值器，因此它不能很好地处理噪声数据，在这种情况下，噪声数据可能是一个复杂的边界形状。
2、计算时间
正如第一段所述，主要目标是减少计算时间，以满足算法执行的实时性要求，耗时比较如下表2所示。
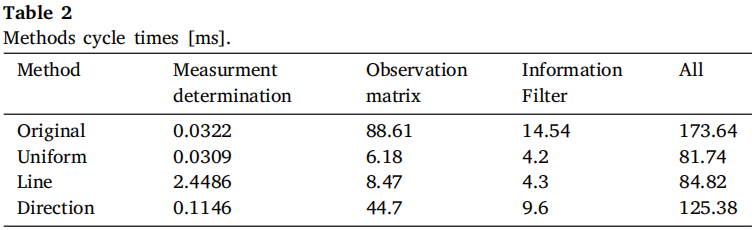
表2的每一行都显示了测试方法的结果，表中只列出了下选影响的PFS算法阶段，乍一看，所提出的解决方案比原始算法至少快1.38倍。在观测矩阵计算中尤其明显，更少的测量次数有助于将该阶段的运行时间提高 14 倍。
3、准确性/质量比较
由于PFS是主动安全系统的一部分，所以可以用分类器来评价，我们可以采用完整的（不是下选的）一组边界像素为参考，则每个逼近样条的点都可以落入以下事件之一：
TP 真阳性 — 偏差（样条点与相应边界点之间的距离）低于定义的最大允许偏差。
FN 假阴性 — 样条点超出参考边界像素之外的最大允许偏差。
FP 误报 — 样条点超出最大允许偏差但在参考边界像素内。
根据上述事件，计算以下指标：
TPR 真阳性率 — 衡量正确识别的实际阳性结果的百分比。
PPV：阳性预测值 — 定义测量的性能。
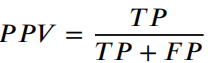
F1：F1 分数 — 是分类准确性（包括精确率和召回率）的综合衡量标准。
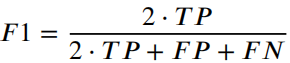
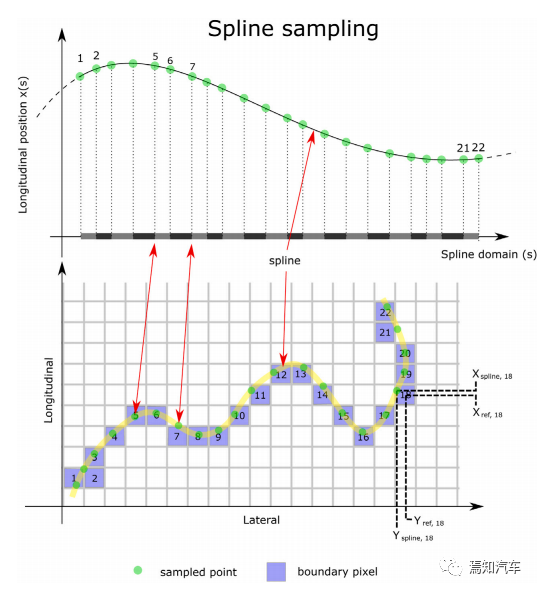
样条采样示例——纵向部分
4、自由空间估计精度
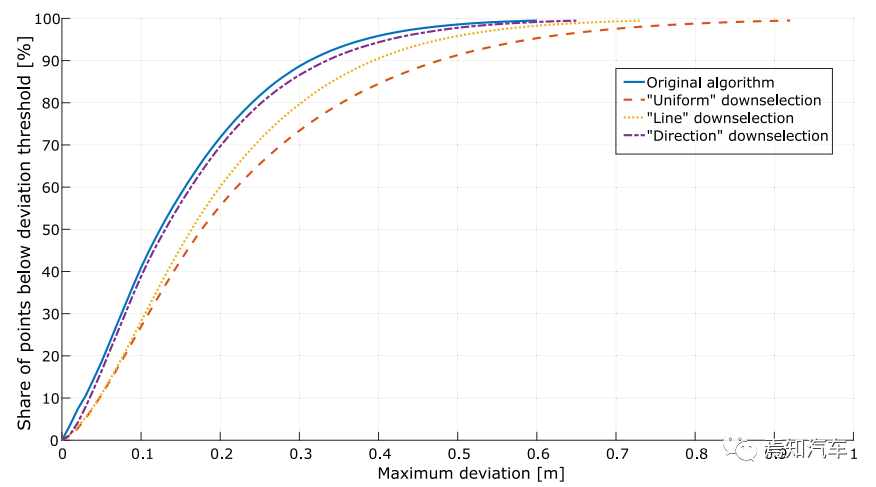
正如预期的那样，根据所使用的测量点的数量，基于“Direction”的算法获得了最好的结果，基于“Uniform”算法获得了最差的几何近似值。为了决定应该采取哪种解决方案，让我们考虑两个质量因子Qtime，它更关注计算时间Qmemory，它专注于内存计算。在这两种情况下，值越高表示结果越好。
Nreduce - 减少的测量点数量
实验表明并证明，对于使用所提出的方法的所有测试用例，PFS 计算中的运行时间和内存需求都可以显着降低，同时可以保持性能（准确性）。这对于资源有限的汽车嵌入式系统非常重要。所提出的下选算法在数据减少、执行时间、准确性和安全性方面进行了比较。总体而言，“线”算法是最有前途的一种。它提供了算法效率（即时间/内存消耗）和性能（准确性）之间的最佳平衡。对于未来的工作中，人们可以研究整个处理流程的其他步骤，特别是图像预处理步骤等方向，因为它仍然是最耗时的部分。
- 用户评论